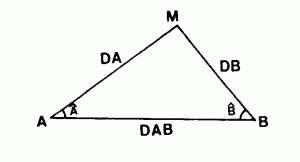
BILATÉRATION (n.f.) Procédé de détermination d’un point isolé M par mesure des distances à partir de deux points connus A, B, sans mesure d’angle.
Voir BILATÉRATION (calcul de) -10,4-.
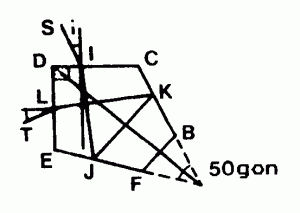
ÉQUERRE OPTIQUE (l.f.) Instrument utilisant la propriété d’un prisme pentagonal dont l’angle D est droit et dont les faces BC et EF argentées font entre elles un angle de 50 gon; la diagonale AD est un axe de symétrie, la face tronquée BF ne joue aucun rôle optique.
Si on considère un rayon incident SI faisant par rapport à la face CD un angle d’incidence i quelconque, le rayon émergent TL a une direction perpendiculaire à SI.
L’équerre optique simple et l’équerre optique double permettent d’appliquer la méthode de LEVER PAR ABSCISSES ET ORDONNÉES.
ÉQUERRE OPTIQUE DOUBLE : Ensemble de deux prismes pentagonaux dont les faces DE sont dans le même plan et qui occupent deux positions tête-bêche.
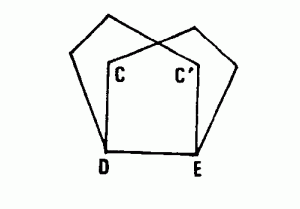
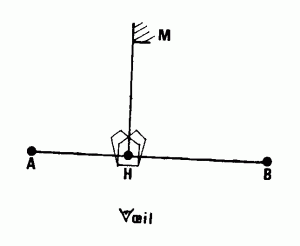
L’équerre optique double permet de se placer à la fois :
* dans l’alignement AB ;
* au pied de la perpendiculaire H abaissée d’un point M sur AB.
ÉQUERRE OPTIQUE SIMPLE : Elle permet, étant sur un alignement AB :
* d’élever une perpendiculaire en H sur AB ;
* d’abaisser la perpendiculaire d’un point M sur AB.
(l.m.) lever des détails M, par intersection d’alignements, tels que FF’ et GG’, F et G étant des points connus visibles de loin, F’ et G’ étant détermines sur la LIGNE D’OPÉRATION -2,2- AB par mesure de distances à partir d’un point I connu sur cette ligne.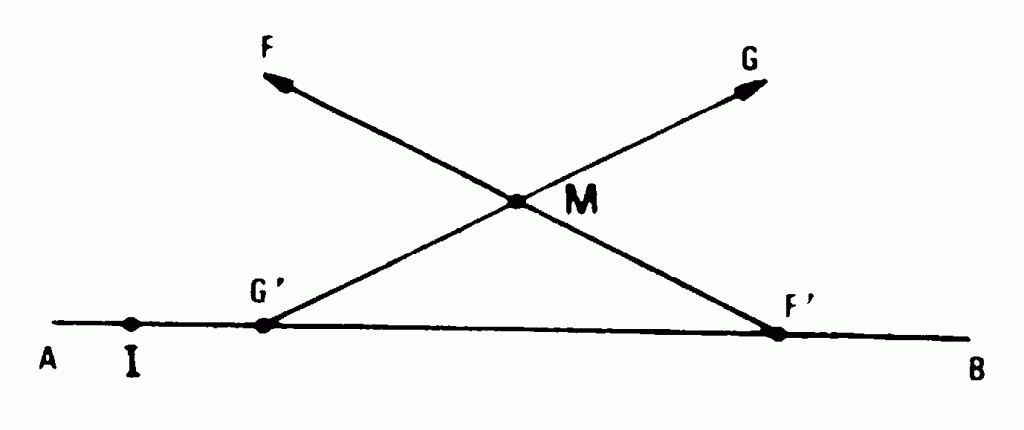
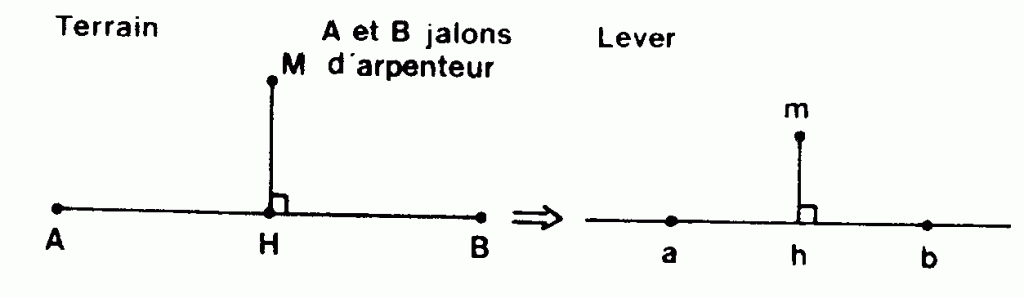
LEVER PAR ABSCISSES ET ORDONNÉES (l.m.) Le procédé consiste à « abaisser » en H, à l’aide de ÉQUERRE OPTIQUE le point de détail M à lever sur la LIGNE D’OPÉRATION -2,2- AB. On mesure « l’abscisse » X = AH et « l’ordonnée » Y = HM. Le report à l ‘ÉCHELLE -1,1- du lever 1/E consiste à déterminer : ah = AH x 1/E, à élever en h la perpendiculaire à ab et y reporter : hm = HM x 1/E.
LEVER PAR FAUSSES ABSCISSES ET ORDONNÉES (l.m.) Le procédé consiste à « abaisser » à vue une quasi – perpendiculaire MI sur une LIGNE D’OPÉRATION -2,2- AB. On mesure X’ = AI, Y’ = MI et la « diagonale » L = AM. On calcule : ![]()
d’où l’abscisse ![]()
1/E étant l’échelle du lever.
On porte ah = x, on élève en h la perpendiculaire à ab, sur laquelle on reporte : ![]()
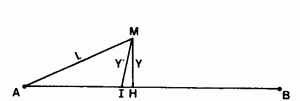
Validité du procédé. On calcule : e = IH = X’ – X puis ![]()
On contrôle que Y et Y’ différent d’une quantité négligeable.
MULTILATÉRATION (n.f.) Procédé de détermination d’un point isolé par mesure de plusieurs distances à partir de plusieurs points connus, sans mesure d’angles.
On calcule le point approché Mo par BILATÉRATION -10,4-. On établit un graphique où l’on trace tous les SEGMENTS DISTANCE -10,4-. Le point définitif M est placé à des distances des segments-distances respectivement proportionnelles aux écarts types de mesure des distances. 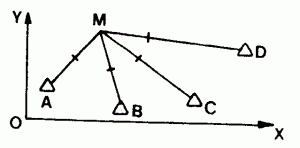
Ce procédé est utilisé en CANEVAS D’ENSEMBLE, -5,1- les longueurs des visées étant déterminées au DISTANCEMÈTRE -2,4-.
QUASI-HAUTEURS (Procédé par) Synonyme de LEVER PAR FAUSSES ABSCISSES ET ORDONNÉES.
TRILATÉRATION (n.f.) Procède de détermination d’un point isolé par mesure de distances à partir de trois points connus, sans mesures d’angles. C’est une MULTILATÉRATION dont le nombre des SEGMENTS DISTANCE -10,4- est réduit à trois.
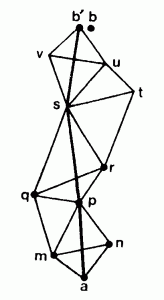
TRILATÉRATION GRAPHIQUE (l.f.) Procédé de lever dans lequel on incorpore les détails dans une série de triangles successifs adjacents dont on mesure les longueurs de tous les côtés au ruban, ainsi que celles d’une série de diagonales telles que AF, PS. SB.
Le report consiste à déterminer le troisième sommet p d ‘un triangle tel que m n p par intersection de deux arcs de cercle de rayons mp = MP/E et np = NP/E centrés sur les deux autres sommets.(MP,NP longueurs mesurées sur le terrain. 1/E échelle du lever ).
Les longueurs des diagonales permettent des vérifications en p,s,b.
Les points A et B reportés en a et b sont connus : on obtient en b un écart de fermeture planimétrique bb’ que l’on compense.