IMPLANTATION D’ARC DE CERCLE PAR RAYONNEMENT
IMPLANTATION D’ARC DE CERCLE PAR RAYONNEMENT (l.f.)
Procédé d’IMPLANTATION PAR RAYONNEMENT -9,3- d’un arc de cercle défini par un point, la tangente en ce point et son rayon R , dans lequel la STATION D’IMPLANTATION -9,1- est sur le point connu et la tangente est prise comme référence. Les COORDONNÉES POLAIRES TOPOGRAPHIQUES – 10,3- de différents points du cercle sont obtenues en donnant à l’angle polaire des valeurs arbitraires : TM : q et r = 2R sin q 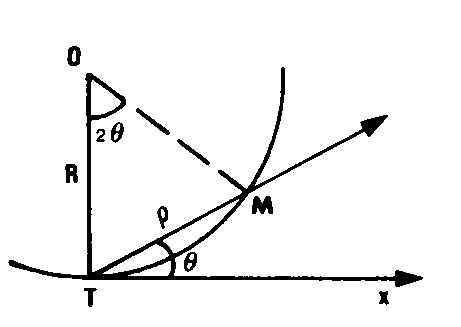 – Si l’on veut implanter des points successifs régulièrement espacés, les valeurs successives de l’angle polaire seront en progression arithmétique: q , 2q , 3q , etc.
– Si l’on veut implanter des points successifs régulièrement espacés, les valeurs successives de l’angle polaire seront en progression arithmétique: q , 2q , 3q , etc.
L’INTERVALLE ANGULAIRE D’IMPLANTATION est alors constant, égal à 2q . 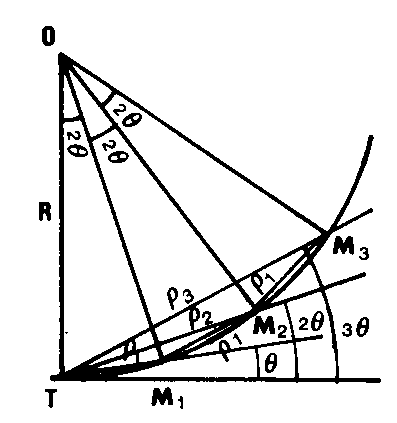 On peut aussi procéder par IMPLANTATION SEMI-POLAIRE -9,3-, car les cordes entre les points successifs sont constantes : r 1 = 2R sin q
On peut aussi procéder par IMPLANTATION SEMI-POLAIRE -9,3-, car les cordes entre les points successifs sont constantes : r 1 = 2R sin q
