RÉDUCTION A L’ELLIPSOÏDE
RÉDUCTION A L’ELLIPSOÏDE (module, coefficient, correction de réduction à l’ellipsoïde)
1) RÉDUCTION A L’ELLIPSOÏDE (l.f.) A partir d’une distance entre deux points, calcul permettant d’obtenir la distance homologue Do sur l’ellipsoïde de référence.
La réduction à l’ellipsoïde peut être effectuée :
* directement à partir de la DISTANCE SELON LA PENTE -2,1-. Voir DISTANCE RÉDUITE A L’ELLIPSOÏDE.
* par l’intermédiaire de la DISTANCE RÉDUITE A L’HORIZON Dh. Dans ce cas seulement on définit les quantités 2.3.4 ci-après.
2) MODULE DE RÉDUCTION A L’ELLIPSOÏDE (l.m.)
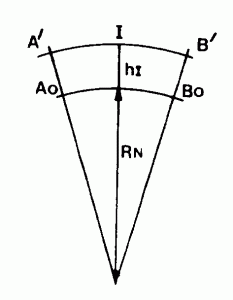
Soit A’B’ une distance réduite à l’horizon, Ao et Bo les projections verticales de A’ et B’ sur l’ellipsoïde de référence. On appelle module de réduction à l’ellipsoïde le quotient de Do = AoBo par :
DhAB = A’B’
mo = Do / DhAB = RN / ( RN + HI) = # 1 – HI / RN
RN : rayon de courbure moyen de l’ellipsoïde sur la ligne Ao Bo,
hI : hauteur de A’B’ au dessus de l’ellipsoïde.
3) COEFFICIENT DE RÉDUCTION A L’ELLIPSOÏDE (l.f.)
Symb : ko
ko = (Do – DhAB) / DhAB = mo – 1 autrement dit, c’est la correction par unité de longueur à apporter à la distance réduite à l’horizon pour obtenir la distance sur l’ellipsoïde. Elle est négative, pour les distances entre deux points situés au dessus de l’ellipsoïde.
4) CORRECTION DE RÉDUCTION A L’ELLIPSOÏDE (l.f.) Correction Co à apporter à la distance déjà réduite à l’horizon : Dh, pour obtenir la distance homologue sur l’ellipsoïde de : Do.
Do = Dh + Co avec Co = ko Dh
