IMPLANTATION PAR DISTANCES (BIPOLAIRES LINÉAIRES)
IMPLANTATION PAR DISTANCES (BIPOLAIRES LINÉAIRES) (l.f)
IMPLANTATION -9,1- d’un point A, à partir des distances à 2 POINTS D’IMPLANTATION -9,1- B et C, le segment BC étant LIGNE D’OPÉRATION -2,2-. 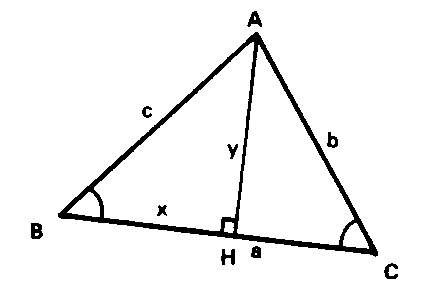
Les longueurs des 3 côtés triangle ABC sont mesurées sur le plan ou déduites des coordonnées de A, B et C. Si on désigne les distances correspondantes sur le terrain, réduites à l’horizon, par :
a = BC, b = AC, c = AB, on calcule :![]() – 1ère méthode : IMPLANTATION PAR ABSCISSE ET ORDONNÉE du point A :
– 1ère méthode : IMPLANTATION PAR ABSCISSE ET ORDONNÉE du point A : 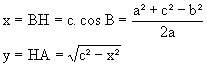 – 2ème méthode : IMPLANTATION PAR RAYONNEMENT du point A :
– 2ème méthode : IMPLANTATION PAR RAYONNEMENT du point A :
En B, depuis le côté BC, on procède à L’OUVERTURE DE L’ANGLE B -9,1- et, dans cette direction, on implante le point A à la distance c.
– 3ème méthode : IMPLANTATION PAR INTERSECTION du point A :
On calcule également l’angle C : ![]() En B et C, depuis le côté BC, on procède à L’OUVERTURE DES ANGLES B et C -9.1- et on intersecte ainsi le point A.
En B et C, depuis le côté BC, on procède à L’OUVERTURE DES ANGLES B et C -9.1- et on intersecte ainsi le point A.
