CLOTHOÏDE
CLOTHOÏDE (n.f.)
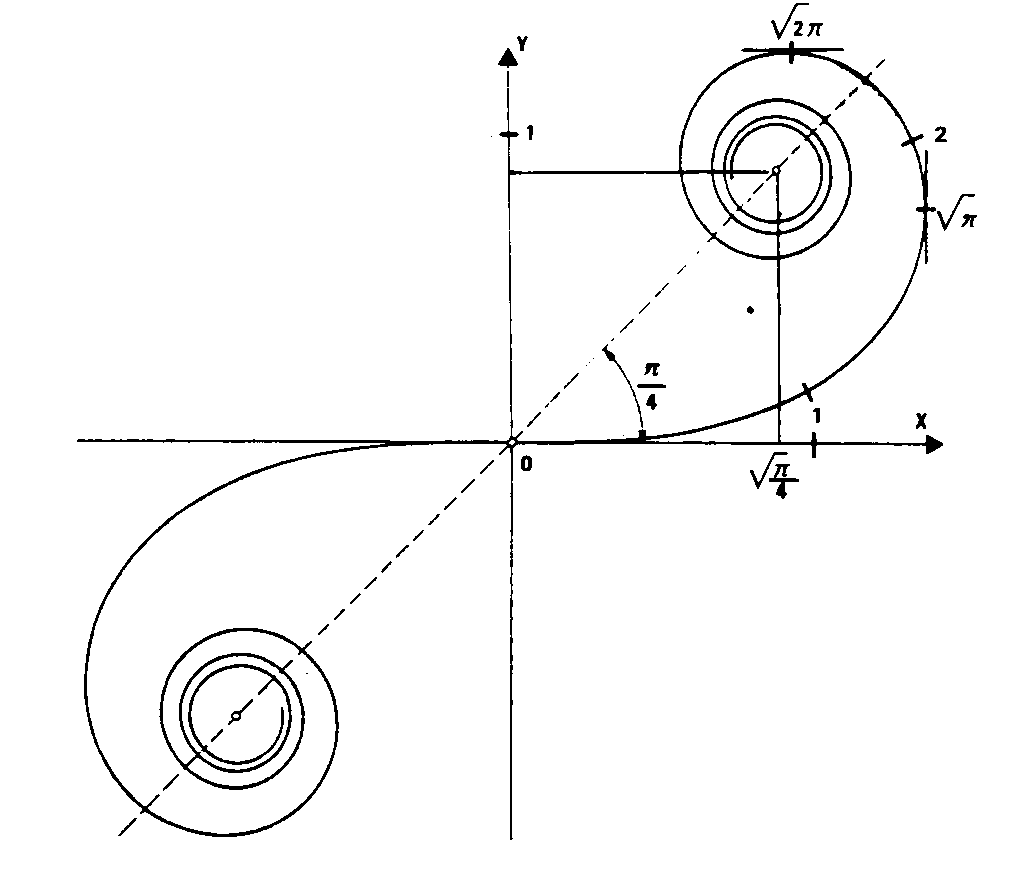
Courbe plane dont la courbure (inverse du rayon de courbure) en un point, varie linéairement avec l’abscisse curviligne comptée positivement et négativement de part et d’autre du point ORIGINE DE CLOTHOÏDE pour lequel la courbure est nulle (point d’inflexion).
Autrement dit, en tout point « M » d’une clothoïde le produit du rayon de courbure « R » par l’abscisse curviligne « S » est constant : R x S = Constante.
Cette constante est homogène au carré d’une longueur « A » appelée PARAMÈTRE DE LA CLOTHOÏDE : R x S = A²
Au point M d’abscisse curviligne « S », le cercle de rayon R ayant même tangente que la clothoïde lui est osculateur ; autrement dit, les deux courbes passent par le même point, ont la même tangente et ont le même rayon de courbure. La clothoïde est extérieure au cercle osculateur vers l’ORIGINE DE LA CLOTHOÏDE, intérieure au cercle du côté opposé.
En un point quelconque d’une clothoïde, le cercle osculateur contient, sans les toucher, tous les cercles osculateurs aux points d’abscisse curviligne supérieure. Une clothoïde ne peut donc admettre comme osculateurs, deux cercles sécants.
Toutes les clothoïdes sont homothétiques entre elles, à une symétrie près par rapport à la tangente au point origine, et en particulier, dans le rapport A, avec la clothoïde « unitaire » de paramètre A = l .