TRIANGLE DE POSITION
TRIANGLE DE POSITION (l.m.)
Triangle de la SPHÈRE DES FIXES dont les trois sommet sont le PÔLE Nord p, le zénith Z et l’astre visé S.
Figure : cas d’un astre à l’Ouest.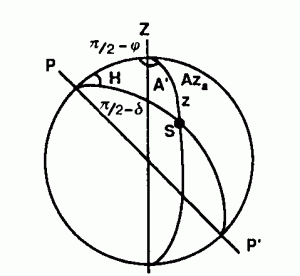
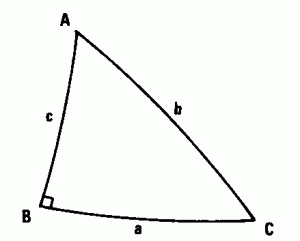
Les 3 côtés sont les arcs :
* a : PS = p /2-d (d DÉCLINAISON DE L’ASTRE)
* b : PZ = p /2-j (j LATITUDE ASTRONOMIQUE du lieu)
* c : ZS = z ANGLE ZÉNITHAL DE L’ASTRE
Les 3 angles au sommet sont :
* A : en Z l’angle d’AZIMUT A’ avec A’ = 400 grades – Az pour un astre à l’Ouest, A’ = Az pour un astre à l’Est.
* B : en S l’ANGLE A L’ASTRE
* C : en P l’ANGLE HORAIRE H
Les 3 côtés a, b, c, et les 3 angles A, B, C, sont liés par les formules de la trigonométrie sphérique. La connaissance de 3 de ces 6 éléments suffit à déterminer les 3 autres.
Quelques formules usuelles classiques, liant les côtés a, b, c et les angles opposés A, B, C d’un triangle sphérique sont rappelées ici.
Formule fondamentale : (1) cos a = cos b ´ cos c + sin b ´ sin c ´ cos a
Formule en cotangente : (2) cotan A=(cotan a ´ sin b – cos b ´ cos C)/sin C
Formule des sinus : (3) ![]()
Par exemple, en topographie, pour calculer l’azimut AZ d’un astre, on part de 3 éléments : les 2 côtés connus PS et PZ (par la déclinaison de l’astre et la latitude du lieu) et un troisième élément observé, qui est, suivant la méthode :
– le 3ème côté ZS : AZIMUT PAR L’ANGLE ZENITHAL (formule 1)
– l’angle compris H : AZIMUT PAR L’HEURE (formule 2)
– l’angle opposé (angle à l’astre), lorsqu’il est droit: Voir: AZIMUT PAR LA DIGRESSION MAXIMALE D’UNE ÉTOILE et AZIMUT PAR LA POLAIRE A SA DIGRESSION MAXIMALE (formule 3 ou l’on fait B = 90° pour obtenir l’azimut).
Dans ce cas d’un triangle sphérique rectangle en B (angle à l’astre), on peut résoudre le triangle, et en particulier calculer l’angle en C (angle horaire) , grâce à la règle mnémonique de Néper: On considère les cinq éléments du triangle (angle droit exclu) dans l’ordre où ils se présentent et en ayant soin de remplacer les côtés de l’angle droit a et c par leurs compléments: 90°- a et 90° – c :
Le cosinus de l’un quelconque des cinq éléments est égal au produit des cotangentes des deux éléments adjacents ou au produit des sinus des deux éléments non adjacents. Par Ex : (4) cos C = tan a . cotan b